如何求解正交矩阵(以例子详细解答)其一
发布于 2021-08-18 16:33:08 浏览 378 次

问题解析:
【】
1、相关推荐
-
-
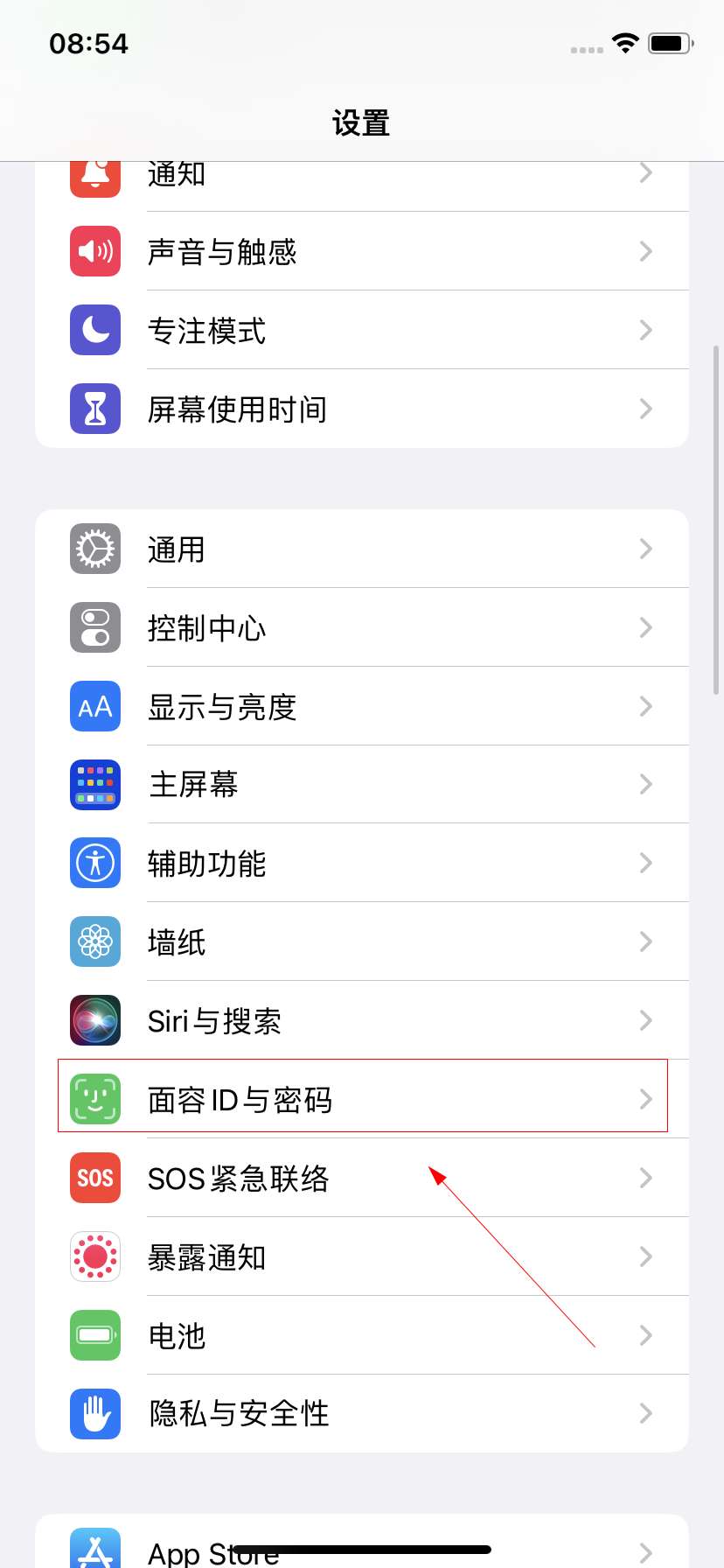
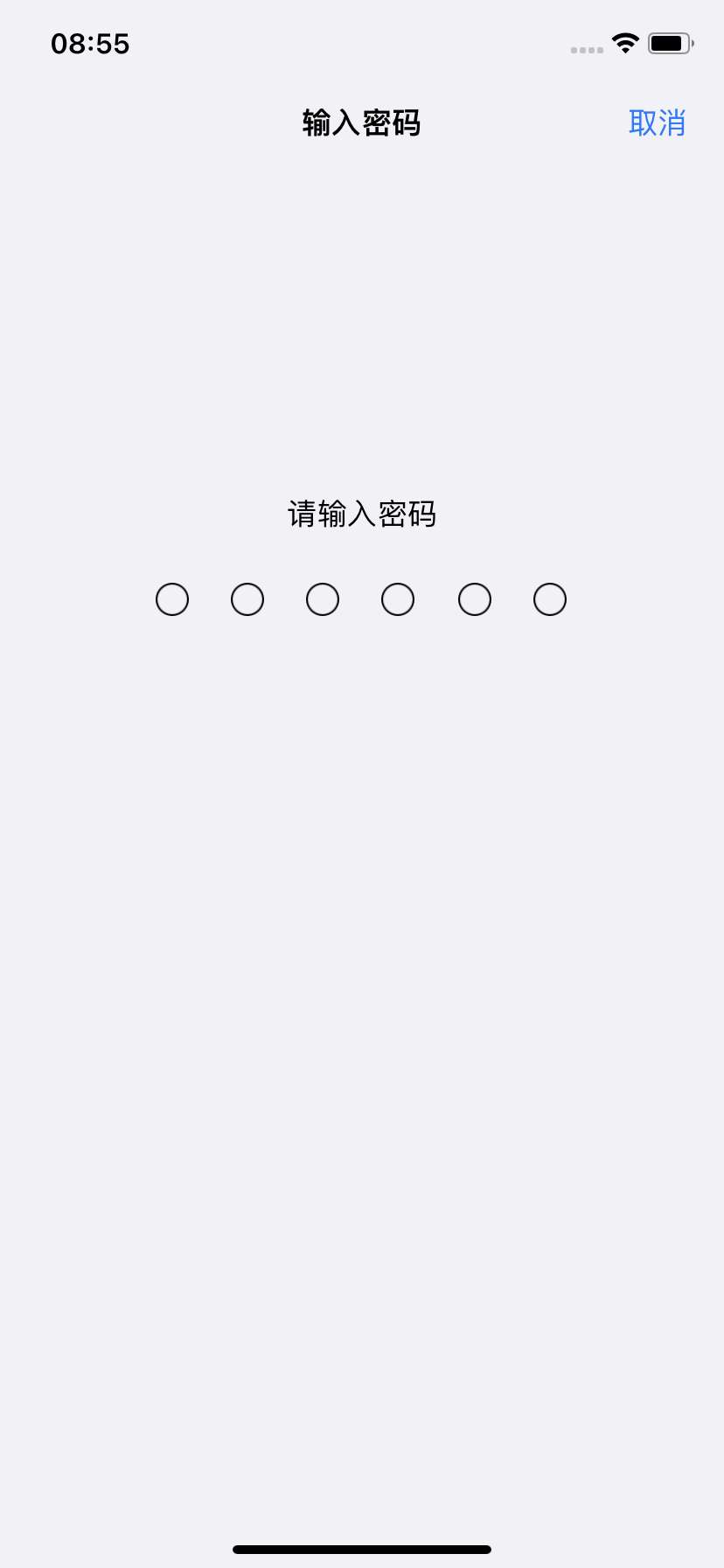
苹果手机如何取消开机密码
-

-
-
- 发布于2022-11-22 08:54:21 935个赞
-
-
-
Amazon如何填写税务信息审查
发布于2022-07-14 04:16:02 1108个赞 -

-
-
-
如何导出SQLServer数据库表到EXCEL
发布于2022-07-13 16:05:54 688个赞 -

-
-
-
如何使用单反
发布于2022-07-08 21:02:06 727个赞 -

-
-
-
oppo手机如何关机重启
发布于2022-06-15 22:45:13 812个赞 -

-
-
-
个人如何在58到家接单
发布于2022-06-15 19:20:44 681个赞 -

-
-
-
微信如何注册公众号
发布于2022-06-15 19:12:59 632个赞 -

-
-
-
微星b450m如何开启Vt
发布于2022-06-15 12:23:58 734个赞 -

-
-
-
电脑如何调手写
发布于2022-06-15 06:15:30 794个赞 -

-
-
-
韩剧tv如何投屏
发布于2022-06-14 11:25:22 551个赞 -

-
猜你可能喜欢
-
-
鸡蛋汤面的制作方法
发布于2024-11-05 11:30:55 767个赞 -

-
-
-
翡翠白玉生煎包的制作方法
发布于2024-11-05 11:30:12 742个赞 -

-
-
-
鱼香肉丝的制作方法
发布于2024-11-05 11:29:15 701个赞 -

-
-
-
鲜掉眉毛的丸子煮干丝的制作方法
发布于2024-11-05 11:28:16 725个赞 -

-
-
-
徽酸菜鱼的制作方法
发布于2024-11-05 11:27:28 755个赞 -

-
-
-
斛参雪梨猪展汤的制作方法
发布于2024-11-05 11:26:11 712个赞 -

-
-
-
滋补鱼头豆腐汤的制作方法
发布于2024-11-05 11:25:11 718个赞 -

-
-
-
鱼头豆腐汤(九阳轻奢炒锅)的制作方法
发布于2024-11-05 11:23:55 613个赞 -

-
-
-
立功东北旧事更新时间
发布于2024-11-04 18:40:35 767个赞 -

-
-
-
《金银》在暗示什么
发布于2024-11-04 18:39:32 800个赞 -

-
